Como recordará del plan de estudios de la escuela en geometría, un triángulo es una figura formada por tres segmentos conectados por tres puntos que no se encuentran en una línea recta. El triángulo forma tres ángulos, de ahí el nombre de la figura. La definición puede ser diferente. Un triángulo también se puede llamar un polígono con tres esquinas, la respuesta será igual de cierta. Los triángulos se dividen según el número de lados iguales y el tamaño de los ángulos en las figuras. Por lo tanto, distinga triángulos como isósceles, equilátero y escaleno, así como rectangulares, de ángulo agudo y de ángulo obtuso, respectivamente.

Hay muchas fórmulas para calcular el área de un triángulo. Elija cómo encontrar el área de un triángulo, es decir. qué fórmula usar, solo tú. Pero vale la pena señalar solo algunas de las notaciones que se usan en muchas fórmulas para calcular el área de un triángulo. Así que recuerda:

S es el área del triángulo,

a, b, c son los lados del triángulo,

h es la altura del triángulo,

R es el radio del círculo circunscrito,

p es el semiperímetro.

Estas son las notaciones básicas que pueden ser útiles si se ha olvidado por completo del curso de geometría. Las opciones más comprensibles y no complicadas para calcular el área desconocida y misteriosa del triángulo se darán a continuación. No es difícil y te vendrá bien tanto para las necesidades de tu hogar como para ayudar a tus hijos. Recordemos cómo calcular el área de un triángulo tan fácil como desgranar peras:

En nuestro caso, el área del triángulo es: S = ½ * 2,2 cm * 2,5 cm = 2,75 cm cuadrados. Recuerda que el área se mide en centímetros cuadrados (sqcm).

Triángulo rectángulo y su área.

Un triángulo rectángulo es un triángulo con un ángulo igual a 90 grados (por lo tanto, se llama triángulo rectángulo). Un ángulo recto está formado por dos rectas perpendiculares (en el caso de un triángulo, dos segmentos perpendiculares). En un triángulo rectángulo, solo puede haber un ángulo recto, porque la suma de todos los ángulos de cualquier triángulo es 180 grados. Resulta que otros 2 ángulos deberían dividir los 90 grados restantes entre ellos, por ejemplo, 70 y 20, 45 y 45, etc. Entonces, recordaste lo principal, queda por aprender cómo encontrar el área de un triángulo rectángulo. Imagina que tenemos un triángulo rectángulo de este tipo frente a nosotros y necesitamos encontrar su área S.

1. La forma más fácil de determinar el área de un triángulo rectángulo se calcula mediante la siguiente fórmula:

En nuestro caso, el área de un triángulo rectángulo es: S = 2,5 cm * 3 cm / 2 = 3,75 cm cuadrados.

En principio, ya no es necesario verificar el área de un triángulo de otras formas, ya que en la vida cotidiana será útil y solo este ayudará. Pero también hay opciones para medir el área de un triángulo a través de ángulos agudos.

2. Para otros métodos de cálculo, debe tener una tabla de cosenos, senos y tangentes. Juzgue usted mismo, aquí hay algunas opciones para calcular las áreas de un triángulo rectángulo que aún puede usar:

Decidimos usar la primera fórmula y con pequeños borrones (dibujamos en un cuaderno y usamos una regla y un transportador viejos), pero obtuvimos el cálculo correcto:

S \u003d (2.5 * 2.5) / (2 * 0.9) \u003d (3 * 3) / (2 * 1.2). Obtuvimos tales resultados 3.6=3.7, pero teniendo en cuenta el cambio de celda, podemos perdonar este matiz.

Triángulo isósceles y su área.

Si se enfrenta a la tarea de calcular la fórmula de un triángulo isósceles, entonces la forma más fácil es usar la principal y, como se considera, la fórmula clásica para el área de un triángulo.

Pero primero, antes de encontrar el área de un triángulo isósceles, averiguaremos qué tipo de figura es. Un triángulo isósceles es un triángulo cuyos dos lados tienen la misma longitud. Estos dos lados se llaman lados, el tercer lado se llama base. No confundas un triángulo isósceles con uno equilátero, es decir un triángulo equilátero con los tres lados iguales. En tal triángulo, no hay tendencias especiales a los ángulos, o más bien a su tamaño. Sin embargo, los ángulos en la base de un triángulo isósceles son iguales, pero diferentes del ángulo entre los lados iguales. Entonces, ya conoce la primera y principal fórmula, queda por descubrir qué otras fórmulas se conocen para determinar el área de un triángulo isósceles.

Un triángulo es una figura geométrica de este tipo, que consta de tres líneas rectas que se conectan en puntos que no se encuentran en una línea recta. Los puntos de conexión de las líneas son los vértices del triángulo, que se indican con letras latinas (por ejemplo, A, B, C). Las líneas rectas que conectan un triángulo se llaman segmentos, que también se denotan generalmente en letras latinas. Existen los siguientes tipos de triángulos:

• Rectangular.
• obtuso.
• De ángulo agudo.
• Versátil.
• Equilátero.
• Isósceles.

Fórmulas generales para calcular el área de un triángulo

fórmula del área del triángulo para longitud y altura

S=a*h/2,
donde a es la longitud del lado del triángulo cuya área se quiere hallar, h es la longitud de la altura trazada hasta la base.

fórmula de garza

S=√p*(p-a)*(p-b)*(p-c),
donde √ es la raíz cuadrada, p es el semiperímetro del triángulo, a,b,c es la longitud de cada lado del triángulo. El semiperímetro de un triángulo se puede calcular con la fórmula p=(a+b+c)/2.

La fórmula para el área de un triángulo en términos del ángulo y la longitud del segmento.

S = (a*b*sen(α))/2,
donde b,c es la longitud de los lados del triángulo, sin(α) es el seno del ángulo entre los dos lados.

La formula del area de un triangulo dado el radio de la circunferencia inscrita y tres lados

S=p*r,
donde p es el semiperímetro del triángulo cuya área se quiere encontrar, r es el radio del círculo inscrito en este triángulo.

La fórmula para el área de un triángulo dados tres lados y el radio de un círculo circunscrito alrededor de él

S= (a*b*c)/4*R,
donde a,b,c es la longitud de cada lado del triángulo, R es el radio del círculo circunscrito alrededor del triángulo.

La fórmula para el área de un triángulo en coordenadas cartesianas de puntos

Las coordenadas cartesianas de los puntos son coordenadas en el sistema xOy, donde x es la abscisa y y es la ordenada. El sistema de coordenadas cartesianas xOy en un plano se llama ejes numéricos mutuamente perpendiculares Ox y Oy con un punto de referencia común en el punto O. Si las coordenadas de los puntos en este plano se dan en la forma A (x1, y1), B (x2, y2) y C (x3, y3), entonces puedes calcular el área de un triángulo usando la siguiente fórmula, que se obtiene del producto cruz de dos vectores.
S = |(x1 – x3) (y2 – y3) – (x2 – x3) (y1 – y3)|/2,
donde || significa módulo.

Cómo encontrar el área de un triángulo rectángulo

Un triángulo rectángulo es un triángulo que tiene un ángulo de 90 grados. Un triángulo sólo puede tener uno de esos ángulos.

La formula del area de un triangulo rectangulo de dos catetos

S=a*b/2,
donde a,b es la longitud de las piernas. Los catetos se llaman los lados adyacentes al ángulo recto.

La formula del area de un triangulo rectangulo dada la hipotenusa y el angulo agudo

S = a*b*sen(α)/ 2,
donde a, b son los catetos del triángulo, y sin(α) es el seno del ángulo en el que se cortan las líneas a, b.

La formula del area de un triangulo rectangulo por cateto y angulo opuesto

S = a*b/2*tg(β),
donde a, b son los catetos del triángulo, tg(β) es la tangente del ángulo en el que se conectan los catetos a, b.

Cómo calcular el área de un triángulo isósceles

Un triángulo isósceles es aquel que tiene dos lados iguales. Estos lados se llaman lados y el otro lado es la base. Puedes usar una de las siguientes fórmulas para calcular el área de un triángulo isósceles.

La fórmula básica para calcular el área de un triángulo isósceles

S=h*c/2,
donde c es la base del triángulo, h es la altura del triángulo bajado a la base.

Formula de un triangulo isosceles de lado lateral y base

S=(c/2)* √(a*a – c*c/4),
donde c es la base del triángulo, a es el valor de uno de los lados del triángulo isósceles.

Como sacar el area de un triangulo equilatero

Un triángulo equilátero es un triángulo en el que todos los lados son iguales. Para calcular el área de un triángulo equilátero, puedes usar la siguiente fórmula:
S = (√3*a*a)/4,
donde a es la longitud del lado de un triángulo equilátero.

Las fórmulas anteriores le permitirán calcular el área requerida del triángulo. Es importante recordar que para calcular el espaciado de los triángulos, se debe tener en cuenta el tipo de triángulo y los datos disponibles que se pueden utilizar para el cálculo.

Área de un triángulo - fórmulas y ejemplos de resolución de problemas

Debajo están fórmulas para encontrar el área de un triángulo arbitrario los cuales son adecuados para hallar el área de cualquier triángulo, independientemente de sus propiedades, ángulos o dimensiones. Las fórmulas se presentan en forma de imagen, aquí hay explicaciones para la aplicación o justificación de su corrección. Además, una figura separada muestra la correspondencia de los símbolos de letras en las fórmulas y los símbolos gráficos en el dibujo.

Nota . Si el triángulo tiene propiedades especiales (isósceles, rectangular, equilátero), puede usar las fórmulas a continuación, así como también fórmulas especiales que son verdaderas solo para triángulos con estas propiedades:

• "Fórmulas para el área de un triángulo equilátero"

Fórmulas del área del triángulo

Explicaciones de fórmulas.:
a B C- las longitudes de los lados del triángulo cuya área queremos encontrar
r- el radio de la circunferencia inscrita en el triangulo
R- el radio del círculo circunscrito alrededor del triángulo
h- la altura del triángulo, bajada hacia un lado
pag- semiperímetro de un triángulo, 1/2 de la suma de sus lados (perímetro)
α - el ángulo opuesto al lado a del triángulo
β - el ángulo opuesto al lado b del triángulo
γ - el ángulo opuesto al lado c del triángulo
h a, h b , h C- la altura del triángulo, bajada al lado a, b, c

Tenga en cuenta que la notación dada corresponde a la figura anterior, por lo que al resolver un problema real de geometría, sería visualmente más fácil para usted sustituir los valores correctos en los lugares correctos de la fórmula.

• el area del triangulo es la mitad del producto de la altura de un triangulo por la longitud del lado sobre el cual se baja esta altura(Fórmula 1). La corrección de esta fórmula se puede entender lógicamente. La altura bajada a la base dividirá un triángulo arbitrario en dos rectangulares. Si completamos cada uno de ellos a un rectángulo de dimensiones b y h, entonces, obviamente, el área de estos triángulos será igual exactamente a la mitad del área del rectángulo (Spr = bh)
• el area del triangulo es la mitad del producto de sus dos lados por el seno del ángulo entre ellos(Fórmula 2) (vea un ejemplo de cómo resolver un problema usando esta fórmula a continuación). A pesar de que parece diferente al anterior, se puede transformar fácilmente en él. Si bajamos la altura del ángulo B al lado b, resulta que el producto del lado a por el seno del ángulo γ, según las propiedades del seno en un triángulo rectángulo, es igual a la altura del triángulo trazado por nosotros, lo que nos dará la fórmula anterior
• El área de un triángulo arbitrario se puede encontrar a través de trabajar la mitad del radio de un círculo inscrito en él por la suma de las longitudes de todos sus lados(Fórmula 3), en otras palabras, debes multiplicar el medio perímetro del triángulo por el radio del círculo inscrito (es más fácil de recordar de esta manera)
• El área de un triángulo arbitrario se puede encontrar dividiendo el producto de todos sus lados por 4 radios del círculo circunscrito a su alrededor (Fórmula 4)
• La fórmula 5 es encontrar el área de un triángulo en función de las longitudes de sus lados y su semiperímetro (la mitad de la suma de todos sus lados)
• fórmula de garza(6) es una representación de la misma fórmula sin usar el concepto de semiperímetro, solo a través de las longitudes de los lados
• El área de un triángulo arbitrario es igual al producto del cuadrado del lado del triángulo y los senos de los ángulos adyacentes a este lado dividido por el doble seno del ángulo opuesto a este lado (Fórmula 7)
• El área de un triángulo arbitrario se puede encontrar como el producto de dos cuadrados de un círculo circunscrito a él y los senos de cada uno de sus ángulos. (Fórmula 8)
• Si se conoce la longitud de un lado y la magnitud de los dos ángulos adyacentes a él, entonces el área del triángulo se puede encontrar como el cuadrado de este lado, dividido por la doble suma de las cotangentes de estos ángulos (Fórmula 9)
• Si solo se conoce la longitud de cada una de las alturas de un triángulo (Fórmula 10), entonces el área de dicho triángulo es inversamente proporcional a las longitudes de estas alturas, como por la fórmula de Heron.
• La fórmula 11 le permite calcular area de un triangulo segun las coordenadas de sus vertices, que se dan como valores (x;y) para cada uno de los vértices. Tenga en cuenta que el valor resultante debe tomarse módulo, ya que las coordenadas de los vértices individuales (o incluso todos) pueden estar en el área de valores negativos

Nota. Los siguientes son ejemplos de resolución de problemas de geometría para hallar el área de un triángulo. Si necesita resolver un problema en geometría, similar al que no está aquí, escríbalo en el foro. En las soluciones, se puede usar la función sqrt() en lugar del símbolo de "raíz cuadrada", en el que sqrt es el símbolo de la raíz cuadrada y la expresión radical se indica entre paréntesis..A veces, el símbolo se puede usar para expresiones radicales simples. √

Tarea. Hallar el area dados dos lados y el angulo entre ellos

Los lados del triángulo miden 5 y 6 cm, el ángulo entre ellos es de 60 grados. Hallar el area de un triangulo.

Solución.

Para resolver este problema, usamos la fórmula número dos de la parte teórica de la lección.
El área de un triángulo se puede encontrar a través de las longitudes de dos lados y el seno del ángulo entre ellos y será igual a
S=1/2 ab sen γ

Como tenemos todos los datos necesarios para la solución (según la fórmula), solo podemos sustituir los valores del enunciado del problema en la fórmula:
S=1/2*5*6*sen60

En la tabla de valores de funciones trigonométricas, encontramos y sustituimos en la expresión el valor del seno 60 grados. Será igual a la raíz de tres por dos.
S = 15 √3 / 2

Respuesta: 7.5 √3 (dependiendo de los requisitos del profesor, probablemente sea posible dejar 15 √3/2)

Tarea. Hallar el area de un triangulo equilatero

Halla el área de un triángulo equilátero de 3 cm de lado.

Solución .

El área de un triángulo se puede encontrar usando la fórmula de Heron:

S = 1/4 raíz cuadrada((a + b + c)(b + c - a)(a + c - b)(a + b -c))

Dado que a \u003d b \u003d c, la fórmula para el área de un triángulo equilátero tomará la forma:

S = √3 / 4 * a2

S = √3 / 4 * 3 2

Respuesta: 9 √3 / 4.

Tarea. Cambio de área al cambiar la longitud de los lados

¿Cuántas veces aumentará el área de un triángulo si se cuadriplican los lados?

Solución.

Dado que las dimensiones de los lados del triángulo son desconocidas para nosotros, para resolver el problema supondremos que las longitudes de los lados son respectivamente iguales a números arbitrarios a, b, c. Luego, para responder a la pregunta del problema, encontramos el área de este triángulo, y luego encontramos el área de un triángulo cuyos lados son cuatro veces más grandes. La razón de las áreas de estos triángulos nos dará la respuesta al problema.

A continuación, damos una explicación textual de la solución del problema por pasos. Sin embargo, al final, la misma solución se presenta en una forma gráfica que es más conveniente para la percepción. Aquellos que lo deseen pueden desplegar inmediatamente la solución.

Para resolver, usamos la fórmula de Heron (ver arriba en la parte teórica de la lección). Se parece a esto:

S = 1/4 raíz cuadrada((a + b + c)(b + c - a)(a + c - b)(a + b -c))
(ver la primera línea de la imagen de abajo)

Las longitudes de los lados de un triángulo arbitrario están dadas por las variables a, b, c.
Si los lados aumentan 4 veces, entonces el área del nuevo triángulo c será:

S 2 = 1/4 raíz cuadrada((4a + 4b + 4c)(4b + 4c - 4a)(4a + 4c - 4b)(4a + 4b -4c))
(ver la segunda línea en la imagen de abajo)

Como puede ver, 4 es un factor común que se puede poner entre paréntesis de las cuatro expresiones de acuerdo con las reglas generales de las matemáticas.
Entonces

S 2 = 1/4 sqrt(4 * 4 * 4 * 4 (a + b + c)(b + c - a)(a + c - b)(a + b -c)) - en la tercera línea de la imagen
S 2 = 1/4 sqrt(256 (a + b + c)(b + c - a)(a + c - b)(a + b -c)) - cuarta línea

Del número 256 se extrae perfectamente la raíz cuadrada, por lo que la sacaremos de debajo de la raíz
S 2 = 16 * 1/4 raíz cuadrada((a + b + c)(b + c - a)(a + c - b)(a + b -c))
S 2 = 4 sqrt((a + b + c)(b + c - a)(a + c - b)(a + b -c))
(ver la quinta línea de la figura a continuación)

Para responder a la pregunta planteada en el problema, basta con que dividamos el área del triángulo resultante por el área del original.
Determinamos las proporciones de área dividiendo las expresiones entre sí y reduciendo la fracción resultante.

El concepto de área

El concepto de área de cualquier figura geométrica, en particular un triángulo, se asociará con una figura como un cuadrado. Para una unidad de área de cualquier figura geométrica, tomaremos el área de un cuadrado, cuyo lado es igual a uno. Para completar, recordamos dos propiedades básicas para el concepto de áreas de formas geométricas.

Propiedad 1: Si las figuras geométricas son iguales, entonces sus áreas también son iguales.

Propiedad 2: Cualquier figura se puede dividir en varias figuras. Además, el área de la figura original es igual a la suma de los valores de las áreas de todas las figuras que la componen.

Considere un ejemplo.

Ejemplo 1

Es obvio que uno de los lados del triángulo es la diagonal del rectángulo, que tiene un lado de longitud $5$ (ya que las celdas $5$) y el otro de $6$ (ya que las celdas $6$). Por tanto, el área de este triángulo será igual a la mitad de dicho rectángulo. el area del rectangulo es

entonces el area del triangulo es

Respuesta: $15$.

Luego, considere varios métodos para encontrar las áreas de los triángulos, es decir, usando la altura y la base, usando la fórmula de Heron y el área de un triángulo equilátero.

Como sacar el area de un triangulo usando la altura y la base

Teorema 1

El área de un triángulo se puede encontrar como la mitad del producto de la longitud de un lado por la altura dibujada hacia ese lado.

Matemáticamente se ve así

$S=\frac(1)(2)αh$

donde $a$ es la longitud del lado, $h$ es la altura dibujada hacia él.

Prueba.

Considere el triángulo $ABC$ donde $AC=α$. La altura $BH$ se dibuja hacia este lado y es igual a $h$. Construyámoslo hasta el cuadrado $AXYC$ como en la Figura 2.

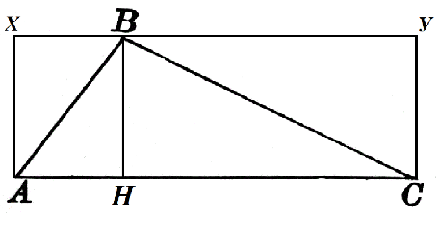
El área del rectángulo $AXBH$ es $h\cdot AH$, y la del rectángulo $HBYC$ es $h\cdot HC$. Entonces

$S_ABH=\frac(1)(2)h\cdot AH$, $S_CBH=\frac(1)(2)h\cdot HC$

Por tanto, el área buscada del triángulo, según la propiedad 2, es igual a

$S=S_ABH+S_CBH=\frac(1)(2)h\cdot AH+\frac(1)(2)h\cdot HC=\frac(1)(2)h\cdot (AH+HC)=\ fracción(1)(2)αh$

El teorema ha sido probado.

Ejemplo 2

Encuentre el área del triángulo en la figura a continuación, si la celda tiene un área igual a uno

La base de este triángulo es $9$ (ya que $9$ son celdas de $9$). La altura también es $9$. Entonces, por el Teorema 1, obtenemos

$S=\frac(1)(2)\cdot 9\cdot 9=40.5$

Respuesta: $40.5$.

fórmula de garza

Teorema 2

Si nos dan los tres lados de un triángulo $α$, $β$ y $γ$, entonces su área se puede encontrar de la siguiente manera

$S=\sqrt(ρ(ρ-α)(ρ-β)(ρ-γ))$

aquí $ρ$ significa la mitad del perímetro de este triángulo.

Prueba.

Considere la siguiente figura:

Por el teorema de Pitágoras, del triángulo $ABH$ obtenemos

Del triángulo $CBH$, por el teorema de Pitágoras, tenemos

$h^2=α^2-(β-x)^2$

$h^2=α^2-β^2+2βx-x^2$

De estas dos relaciones obtenemos la igualdad

$γ^2-x^2=α^2-β^2+2βx-x^2$

$x=\frac(γ^2-α^2+β^2)(2β)$

$h^2=γ^2-(\frac(γ^2-α^2+β^2)(2β))^2$

$h^2=\frac((α^2-(γ-β)^2)((γ+β)^2-α^2))(4β^2)$

$h^2=\frac((α-γ+β)(α+γ-β)(γ+β-α)(γ+β+α))(4β^2)$

Como $ρ=\frac(α+β+γ)(2)$, entonces $α+β+γ=2ρ$, por lo tanto

$h^2=\frac(2ρ(2ρ-2γ)(2ρ-2β)(2ρ-2α))(4β^2)$

$h^2=\frac(4ρ(ρ-α)(ρ-β)(ρ-γ))(β^2 )$

$h=\sqrt(\frac(4ρ(ρ-α)(ρ-β)(ρ-γ))(β^2))$

$h=\frac(2)(β)\sqrt(ρ(ρ-α)(ρ-β)(ρ-γ))$

Por el Teorema 1, obtenemos

$S=\frac(1)(2) βh=\frac(β)(2)\cdot \frac(2)(β) \sqrt(ρ(ρ-α)(ρ-β)(ρ-γ) )=\sqrt(ρ(ρ-α)(ρ-β)(ρ-γ))$